30 Sep 2017

a home grown tree

Data scientists really do get spoiled these days. With a wealth of high quality libraries readily available there quite often a ready built solution available to whatever your problem may be. This can lead to the modeling being somewhat taken for granted in many cases, with the real focus being on feature engineering.

I think this is a shame, and in extreme scenarios can lead to practitioners who have merely memorised the API to R's caret package or Python's Scikit-Learn to declare themselves to be an expert in machine learning.

Now, while I would never suggest that reinventing the wheel and implementing a suite of learning algorithms from scratch would be a constructive use of time in normal circumstances, I do feel that having a decent understanding of how learning algorithms work leads to much higher quality outputs. Further, it provides you with the knowledge to tackle problems that don't lend themselves easily to an off-the-shelf solution.

I would compare an excercise such as this to a musician practising their scales and arpeggios: they would never be performed in a concert, but certainly improve the musician's skills and ability.

As always, my code is in a repository so that you can have a look, improve it, or criticise :)

Overview

In this post I will run through some of the key ideas to implement a tree class in Python. I won't be focusing on performance, and I won't be working as cleanly as Scikit-Learn does, working purely off numpy arrays (I found Pandas dataframes more expressive for this exercise as I am working with labelled data). The focus will be on the algorithm, not producing some highly optimised software library.

Right, now most people reading this blog will have at least a rough notion what a decision tree is. A tree can be collapsed into a series of if-then statements (rules): you start at the root, and then based on the feature values of your sample you work your way down to leaves which will give you the final classification. I can point you to books such as The Elements of Statistical Learning by Hastie et al, or Applied Predictive Modeling by Kuhn and Johnson for a decent overview on the subject.

So we have two challenges. Firstly, we must grow a tree with some training data. Once the tree is grown, we must be able to make predictions, that is, feed through new samples and obtain an outcome.

Node class

We will start by defining a node class. Our tree will be composed of a list of nodes. It's quite simple to code up:

class Node(object):
    '''
    representation of a node in a tree
    '''
    def __init__(self, index, depth, parent, direction,
                 is_leaf, left_child_ix, right_child_ix,
                 split_feature, split_value, metric_score,
                 class_counts):
        self.index = index
        self.depth = depth
        self.parent = parent
        self.direction = direction
        self.is_leaf = is_leaf
        self.left_child_ix = left_child_ix
        self.right_child_ix = right_child_ix
        self.split_feature = split_feature
        self.split_value = split_value
        self.metric_score = metric_score
        self.class_counts = class_counts
        self.pruned = False

All a node object does is hold as attributes the information we need for our tree. When we grow our tree, we will represent it as a list of nodes. The index attributes of the a node object (index, left_child_ix and right_child_ix) refer to the node's position and the postion of its children in the list representation of our tree.

For brevety, I won't dwell too long on the Node class- all the attributes will make sense as we move on to discuss the Tree class.

Tree class

Now the tree class is a little more involved. For you to follow along, check out the code in the repository.

Firstly, whats the intuition for growing a tree? We start by considering all our data, and we split it so that the resulting groups are 'more pure' in terms of their classification values than previously. We will measure the purity before and after the split using the Gini Index. To decide where to split, we have to consider all possible splits for all the features describing the data, and we take the one that gives us the purest resulting groups.

And then, we do it again. And again. And again. Growing a tree lends itself naturally to a recursive algorithm, and are often referred to as recursive partition trees. The process is rather straightforward if you are used to recursive algorithms, and can be a bit of a mind warp if not. But what better way to get to grips with recursion? This process is implemented in the __rpart() method of the Tree class.

The __rpart() method builds the tree following a preorder traversal scheme, which is a fact I use to represent the tree as a list of nodes.

The partitioning process should have stopping criteria as well- you can't go on forever. At the very least, you will want to stop when you get to a pure node. In fact, trees can be quite susceptive to overfitting and therefore can generalise poorly to previously unseen data. Therefore, it is common to terminate the tree growning at a prescribed depth, or when the number of samples in a node drops below a threshold. In my implementation, I give the user the ability to define the maximum depth of the tree.

I gather the neccessary steps to grow the tree in a grow_tree() method, which looks like the following:

def grow_tree(self, df, features, target, prune = True):
    #
    # how many unique classes in the outcome?
    self.n_cls = df[target].value_counts().shape[0]
    #
    # recursive partition
    self.__rpart(df, features, target, depth=0, parent=None)
    #
    # add child node indices by inspecting parents
    for i in range(len(self.nodes)):
        tmp = [x for x in self.nodes if x.parent == i]
        if tmp == []:
            self.nodes[i].left_child_ix = None
            self.nodes[i].right_child_ix = None
        else:
            LC = tmp[0].index
            RC = tmp[1].index
            self.nodes[i].left_child_ix = LC
            self.nodes[i].right_child_ix = RC
    #
    # We can prune the tree to prevent overfitting
    # A very simple scheme has been implemented
    if prune:
        self.__prune()
    #
    self.is_grown = True

Essentially, once we have finished the partitioning, we have to perform a scan of the list of Node objects to insert the child indices of each node by considering the parent. The __rpart() method could possibly be updated to capture this information at the time of the recursive partitioning, but this was the most simple approach I could think of to update this information in the tree representation. The grow_tree() method then calls __prune(), which implements a simple pruning scheme.

Pruning is a common measure that can be taken against overfitting. To do this, I start from the leaves of the tree, and check to see if the split that lead to the leaf actually improved the overall performance of the tree. I enqueue all the leaf nodes, perform the check, and then if I decide to 'prune' at the leaf's parent, I make the parent a new leaf and add it to the back of the queue to be processed. You can check out my __prune() method, and if you are interested you can investigate more advanced pruning schemes.

Finally, now the tree is grown, how do we predict? The simplest way I could think of is to pass the features as a dictionary, and then follow the rules to a leaf starting from the root. The predict() method optionally returns either a hard classification by returning the majority class in the leaf, or a pseudo probability by returning the proportion of each class in the leaf.

In case you missed it, the code is here- have a look if you are interested!

Test run: the iris data set

I have put together a little demo here using the trusty iris data set.

Initially, I consider two features to make the visualisation easy. After initialising a tree object, specifiying maximimum depth of 3, I fit to the data using petal length and petal width as features. Note that this is just for a demonstration, so I havent bothered with a train/test split or any cross validation for hyperparameter selection.

Once I have fit the tree, I predict the class outcome over all feature space using a grid of points. The resulting classification boundaries can be seen below, along with the training data:

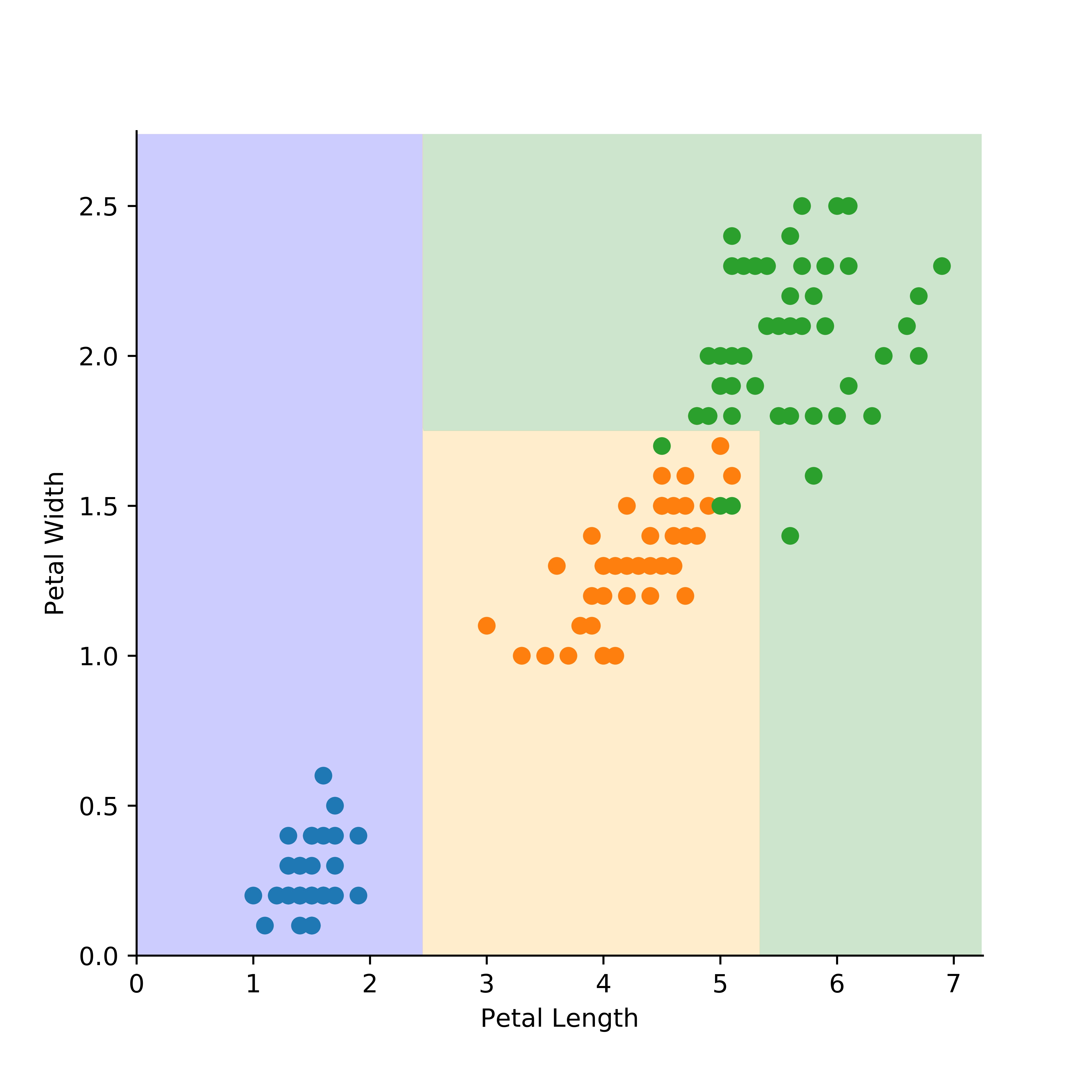
In the above, the different colour circles correspond to the species of iris, and the shaded regions correspond to the classification regions. If you used the model to predict a new observation, the outcome would correspond to where it lies in (petal length, petal width) co-ordinate space.

We see that there would be some misclassifications using this model, due to the overlap of two of the species. This is to be expected in this two dimensional example, and in fact we would be suspicious of overfitting if we perfectly fitted the training dataset.

As a final example, to demonstrate that the model can generalise to >2 features, I fit another model using all four features. This time, I perform a train/test split. As you can see at the bottom of the notebook where I produce a confusion matrix of the test set predictions, we have two classification errors on the test set. Unsurprisingly, this is for the second and third species, which we saw to overlap slightly in feature space.

Other thoughts

So there we have it- a classification tree! A fun, educational little exercise. Hopefully you found it informative if you had ever wondered how to implement such a model yourself.

This could be easily extended to a random forest classifier, one of the most powerful and well-known supervised learning algorithms. I'll write a part II to this post soon!

TL;DR- I implemented a classification tree model in Python. The code is here