31 Oct 2017

A random forest of trees

In my previous post, I described how you might implement a decision tree classifier in Python, and demonstrated its usage on the iris data set.

In this post, we will adopt Leo Brieman's methodology to create a random forest ensemble model out of trees. The methodology is suprisingly straightforward to implement considering how powerful and widely used the model is.

As always, my code is available in a repository if you want to dive in!

Methodology

The methodology I will adopt to construct a basic random forest of m trees, considering a data set with P features is the following:

• For each tree, generate a bootstrap sample of the original data
• Train a tree on this data, at each split considering a random subset of the P features. Do not prune the resulting tree.

One very useful consequence of this approach is that individual trees can be much less computationaly intensive to train, as we only consider a subset of the total number of features at each split. Of course, we have to train many trees, but in principle this can be done in parallel.

The bootstrap resampling and random selection of splitting features leads to decorrelation of the trees in the forest. When making predictions, a vote is cast between each of the m trees- that is, they each make a prediction of the outcome class and the majority wins. A pseudo probability can also be obtained by considering the proportion of votes for each class.

Brieman and Cutler's original implementation is written in Fortran, and available here should you like a go at digesting it.

Implementation

My implementation of a RandomForest class is a simple composition class using the Tree class I implemented in my previous post. My strategy is to train and store an ensemble of trees when I train the RandomForest object. When I make predictions using the predict() method, I predict for all trees in the ensemble, take a vote and return the majority class.

The after we have initialised the object, we use the grow_tree() method to train the model. The method looks like this:

# train our model by growing forest of trees on training data
def grow_forest(self, df, features, target, seed = 1234):
    #
    # total number of outcome classes
    self.n_cls = df[target].value_counts().shape[0]
    #
    # set seed for consistent results
    np.random.seed(seed)
    #
    # Grow forest
    # This is an obvious candiate for parallel processing
    for i in range(self.ntrees):
        #
        # create bootstrap sample of data
        # we train on those 'in bag'
        # in principle we could use 'out of bag' for validation
        # but we don't do that here
        df_ix = df.index.values
        bag_ix = np.random.choice(df_ix,
                                  size = df_ix.shape[0],
                                  replace = True)
        oob_ix = np.setdiff1d(df_ix, np.unique(bag_ix))
        #
        # randomly select mtry features
        feature_ix = np.random.choice(np.arange(len(features)),
                                      self.mtry,
                                      replace = False)
        curr_features = [features[x] for x in feature_ix]
        #
        # initialise Tree
        tree = Tree(max_depth = self.max_depth,
                    metric = self.metric)
        #
        # grow unpruned tree
        tree.grow_tree(df.loc[bag_ix, :], curr_features, target, prune=False)
        #
        # add tree to forest
        self.trees.append(tree)

The predict method is rather straightforward, so I will skip discussion for brevety here. Of course, the full code is here if you would like to see it.

As you saw in my previous post, I do not claim that this implementation will be fast or efficient. This exercise is purely for education, and if you want an efficient implementation of a random forest model, I suggest using the implementation in Scikit-Learn which has the heavy number crunching written in C.

Test

For testing, I decided to consider a harder case than we looked at when we tested the Tree class. Here, we can still use the iris data set, but consider a harder example where the classes are not well seperated. This will force our model to demonstrate how flexible it can be.

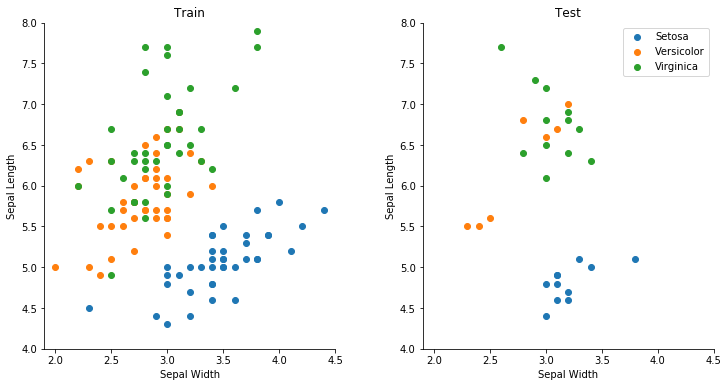
Here, when considering sepal length and width, we see that Setosa is clearly separated, but there is a region where it is virtually impossible with the available data to build a model to distinguish Versicolor and Virginica. The left plot shows a training dataset, and the right shows a holdout for testing our final model.

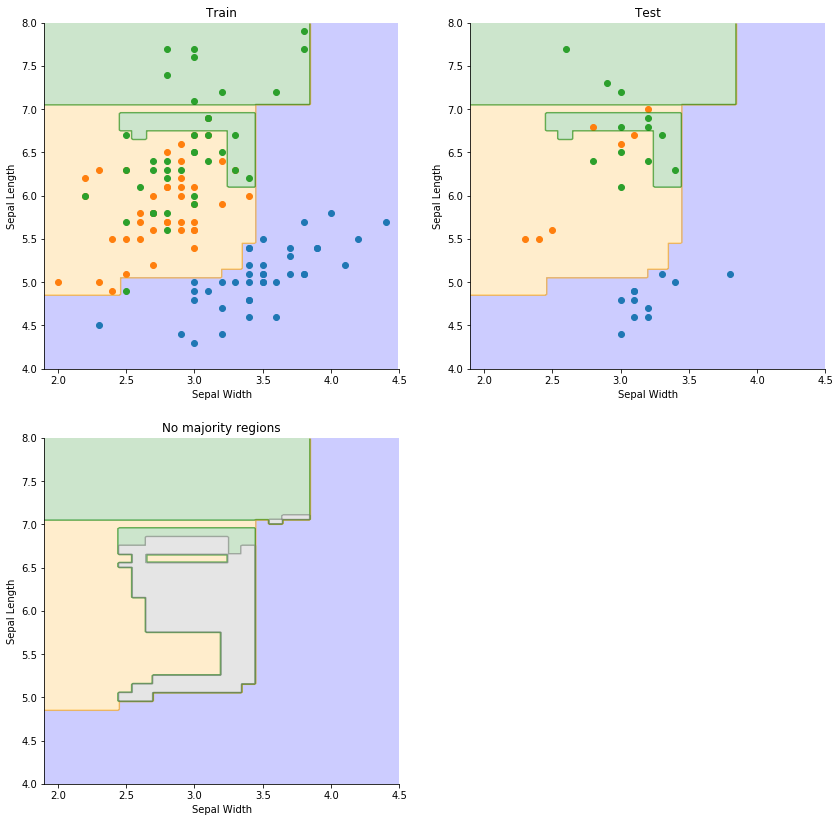
A random forest is capable of fitting flexible decision boundaries, so it is wise to take precautions against over fitting (i.e. it will not generalise well when making predictions on data it was not trained on). Therefore, after performing cross validation, we settle on using 25 trees of a max depth of 8, considering both features at each split. This achieves 83% accuracy on the test set. Do bare in mind, however, that the test set is rather small, and probably not the best representation of how well the model generalises.

We can plot the resulting decision boundary with the train and test data. A final region is plotted to show the areas where the majority vote is less than 0.5: this tells us we have limited confidence in any predictions in these regions.

We can chose to interpret the proportion of votes as a kind of 'psuedo probability', and visualise this instead of hard classifications. I call this as a 'pseudo probability' as I have not checked if it can be interpreted as a probability in a statistical sense. I would investigate calibrations to do this, but I'll leave that out to stop this post getting too long!

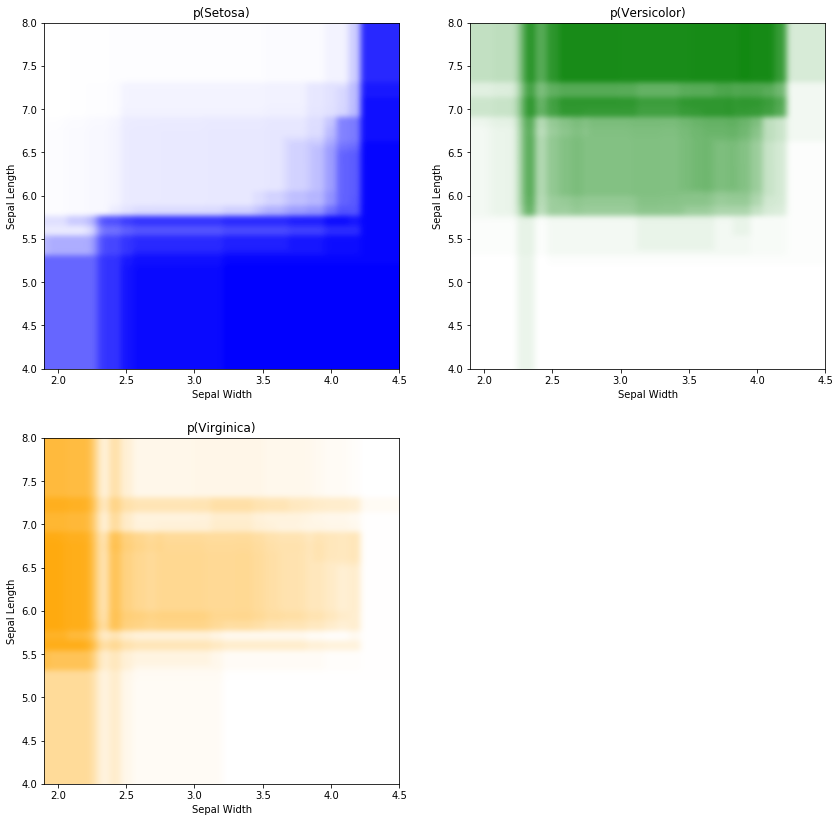
As we can see, the central region competes mainly between the Veriscolor and Virginica classes, but there is a small proportion of Setosa votes in the ensemble as well. I would be suprised if any model could actually perform that well in the central region due to the class overlap and relatively small amount of training data. This is a nice example of data being the differentiator, not the model. In other words, we are in a garbage in, garbage out scenario- if you don't have useful data, regardless of the complexity of the model you use, you will struggle to build something useful.

Other thoughts

So there we have it, a simple implementation of a random forest classification model. I am always amazed how such a simple heuristic performs so well in practice. Random forests come with other advantages, such as being incredibally robust to non informative or correlated predictive features, often meaning that minimal preprocessing is required. Also, data doesnt require scaling if features are on different scales. You can even get a notion of feature importance by considering how often a feature is chosen for a split.

Overall, this has been a fun little extension to wrap up my previous investigation of tree based models (unless I decide to come back andimplement a boosted tree model). To reiterate, I would never use this implementation in practice (I would use a tested, optimised implementation in a library). However, understanding how models work will make you much more effective if you do predictive modelling for a living!

TL;DR- I implemented a random forest classifier based on the decision tree classifier I built in a previous post. The code is here.